今日のテーマは小学校受験の「図形」です。
受験対策で色々取り組んできた中で、躓きやすい問題の解き方、これまで使って良かった教材のご紹介をしていきたいと思います。
図形問題は、幼児期から小学校期にかけて優良な教材がたくさんありますが、小学校受験から大学受験に至るまで、どのフェイズにおいても重要であり、差がつく論点です。
小学校受験の図形論点
小学校受験の図形論点は下記の通りです。
パターン問題も多いですが、奥が深く、幼少期に身に着けたスキルは「図形センス」と一くくりにされることも多く、一朝一夕では身につかない点が特徴的です。
年齢別の学習教材
取組の成果を挙げておかないと説得力がないので、一部挙げておきます。
私自身、幼児期に学研のニューブロックで遊んでいたことは覚えており、人並に色々と考えてくれていたことは親の感謝です。娘にはこの経験と反省をふまえ、色々なものを体験してもらいました。
この結果、小学校受験においても図形問題で点数を稼ぐことが多かったです。
このため、幼児期の図形に関しては、成果を出すにあたり、色々なことに取り組んだ中で何かしら理由があるはずです。
図形問題の解き方を交えつつ、一つ一つ振り返っていきます。
図形問題の解き方
基本と応用に分けて説明していきます。
基本
まず、年少~年中にかけて、下記を重点的に抑えてください。
点図形は点を結んでいくだけですが、正確で迅速な運筆能力が求められます。
この能力は、色々な図形問題を解く上で必要な基礎となります。
線対象もまた、紙を切り抜きした際にどのような形になるか、など他の問題を解くための基礎となります。
点対称も線対象が解ければ解けるようになります。
回転図形は、立方体の90度回転がまず基本となります。
これができれば2回回ったらどうなるか。左に回る時はどうなるか、4回回れば一回転することなど理解が広がっていきます。
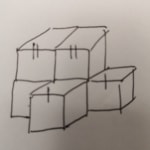
立方体は積み木の数の数え方を理解すればあとは数えるだけです。
具体的には上図の通り、上からみた合計の数をメモして、最後に数えるだけです。
頻繁に出題されますが、確実に得点することで自信になります。この数え方は最後まで役立ちます。
年中の前半までは、年齢相応の内容しかできなくて当然です。
一部教室ではスピードを上げて優位性を保とうとしますが、ついていけない場合は無理せずにお子様のペースを大事にしてあげてください。ここで勉強嫌いにならないようにケアする点が重要です。
応用

年中後期から年長にかけて、徐々に問題が難しくなっていきます。
上記基礎に続いて取り組みやすいのはブラックボックス、系列など。
その後、展開図などに繋がっていきますが、展開図は小学校受験において難問です。
ここで娘が苦労した問題を事例に、解き方を説明しておきます。
立方体の四つ折りを切った場合の展開図です。上図の通り切り取り線で切った場合、紙は何枚になるかわかりますか?この問題はこぐま会の一般書籍の問題集にある問題です。色々な問題にも応用できる良い問題と思います。
この手の問題の定石は実際に切ってみる、という手法がメジャーですが、このレベルになるとなかなか大変で、一回では解けるようにならないことが多いです。
この点、丸覚えに頼らない法則はあります。
下記の通り色分けして考えてみます。
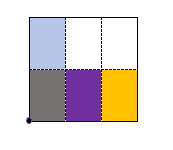
これを開くと、下記のようになります。ここで線対象の知識を使います。
折り目を開く時、線対象となる部分のうち、点線ではない部分(折り目の部分)は二つになりません。
このため、色付きの部分を1枚として考えてみてください。白い部分は折り目がありませんので、折り目を開くたびに数が増えます。この合計が答えです。
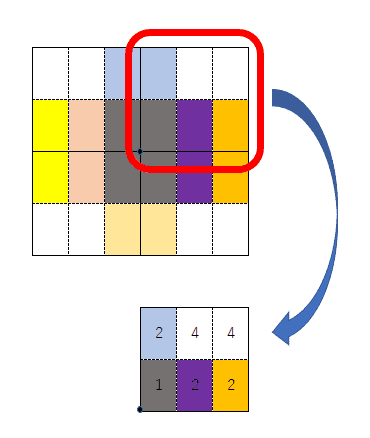
上記、白の数と色別の数を全て足すと15枚。難しいですね。
丸暗記だともったいないので、この過程を見せたあと、最終的に下記のように説明すると良いです。
①折り目の軸は二回開いてもくっついている。→黒部分は1枚だね。
②折り目が片方だけあるとき、折り目がない時だけ増える。→他の色付き部分は2枚
③折り目がどこにもないものは、開くたびに増える。→白色部分は1枚→2枚→4枚
ここでまだピンとこない事もあると思います。
数字を使わない場合、全体の図を書き、下図のように手を繋いでいると教えて、鉛筆でつないで数えるのも良いですね。
これは私のオリジナルですが、この考え方を基に、数字が書けるようになったら上の解き方に移行すると、展開図も意識した丸覚えに頼らない理解ができます。
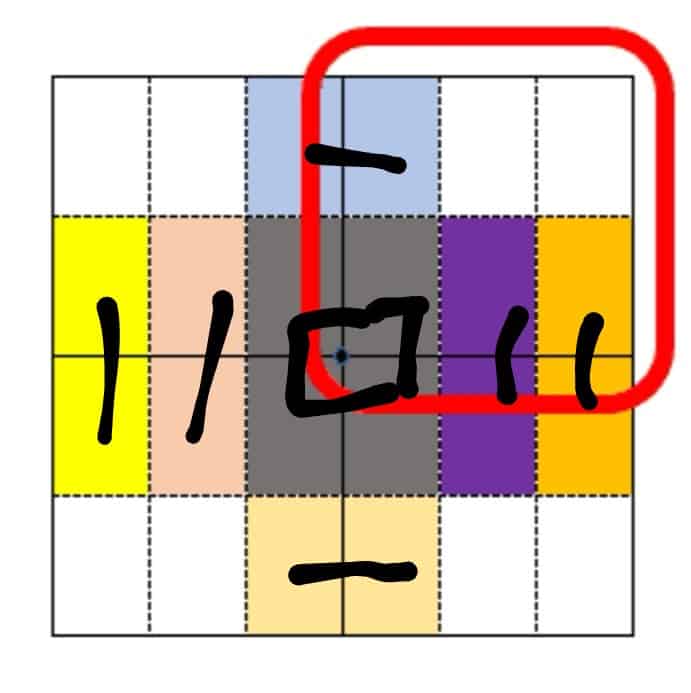
ここまでわかっていると、仮に点線部分が増えてもある程度対応できます。
もう一点、変わり種として抑えておきたい点は、軸を通って斜めに切った場合はどうなるか。
でも、上記法則がわかっていれば対応できます。
上記①がなくなり、②に該当しますね。二回開くうち、一回分だけ折り目があります。
よって、2枚が2セットとなり、合計4枚となります。
回転に係る応用はややマニアックな問題も含まれますが、これまでの応用で解けます。
例えば、途中で崖になっていて、壁にくっつきながら回転する場合。この場合はいくつか解き方がありますが、崖の直前の軸を基に、点対称で解けますね。
合成もよく出題されます。色々なパーツを組み合わせて特定の図形を作る問題。この問題は結構厄介ですが、幸い優良な教材が溢れています。後述しますので参考にしていただければと思います。
幼児期に取り組んだ図形教材
パズルよりはタングラムが好き
娘には一生懸命パズルを与えていて、2ピースから地道に一緒に取り組んだりもしましたが、そこまでドはまりはしませんでした。
残念ながら。しかしながら、なんとか解けるレベルのタングラムは面白いようです。
タングラムは解けない苦しさと、解けた時の満足感が常に同居します。
前者が勝てばやめてしまうでしょうし、解けてきて自信につながると、どんどん先へ進めていきます。
タングラムでおすすめは公文のタングラムです。
おもちゃ屋でも買えますし、ネットで割安で買うことができます。
過去のブログでも触れています。

最初はたった2ピースの組み合わせから始まり、3ピースになると考える問題が多く、ボリュームもあるので、ここが一つの壁となります。それ以上になると、意外にも簡単に解けるものが多いです。これは基礎的な組み合わせが3ピースにたくさん存在し、これを使えば他にも応用できることがわかってくるからと考えます。
タングラム的な図形の組み合わせ問題は、小学校受験でも必須の問題となります。
ニューブロックは親子2世代で利用
親子で取り組むことになった歴史あるニューブロック。
こちら、形が独特で、立方体を作ったり、曲線の棒やタイヤを使って車を作ったり、発想は様々。
ブロックもまた微妙に柔らかくて、触り心地も良いんですよね。
ニューブロック自体は成績向上や、小学校受験にも直接紐づけられる関係性はわかりませんが、想像力を豊かにしてくれる面で優良な知育玩具です。
パターンブロックの活用
パターンブロックは、国立小、私立小の先生方が推薦することが多い教材です。
それぞれの角度を肌で感じながら、幼児が好きな通り、ぴったり合う図形を作っていきます。
パターンブロックはピースが小さいので、巧緻性向上にもつながります。
しかし、、こちらパターンブロックは自宅では他教材に比べてやや放置され気味でした。
というのは、直接的に出題される傾向がそれほどでもないためです。
この点、パターンブロックや図形を重視する知能系の幼児教室へ通うことで、学習習慣ができました。
図形はいざやってみると面白いのですが、その面白さがわかるまでは時間がかかりますので、きっかけを与えてくれたかもしれません。幼児教室の有用性は、そこで何を習うかというより、興味を引き出すことと考えます。
動画で学ぶ
今年4月からお世話になっているワンダーボックスは、親子でお世話になっています。
今のところ、小学校受験に適した図形センスを磨けるタブレット教材は、ワンダーボックスとシンクシンクがずば抜けています。
小学校受験では運筆能力も重要ですから、動画が動いて展開図や回転が理解できるなど、それなりの質がなければ紙の方が良いです。いかに鉛筆を使って正確に素早く解く練習をこなすかが重要ですから、タッチパネルの場合、単純な小学校受験の数の問題や、積み木の数などは避けたいところ。
シンクシンクはアプリ専門、ワンダーボックスはアプリに教材を加えたSTEM教材ですが、子供の感覚では「遊び」になることが多く、親としては非常に楽です。休憩時間、移動時間に愛用していました。
従前の教材と違う点は、自由な発想で、様々な種類の問題を、動画で動きを確かめながら学べるという点でしょう。
小学校受験で言えば、サイコロがコロコロ右左に転がって、スタンプがあるマスはどこでしょう!
という理不尽な問題がありますが、そのような問題も収録されています。
この問題、私より解くのが早くなりました。合理的な方法ではなく、感覚で解いています。
アプリの構成は下記の通りで、簡単な問題から徐々にステップアップしていく仕組みになっています。
小受では何かとお金がいりようですが、図形問題に関しては、幼児教室に多額の費用を払う必要ないと考えます。
実際にかなりやりこんでいる記録はこちら↓
【2020年】Wonderbox(ワンダーボックス)で実際に遊んだアプリランキング | まなのび:幼児教育と教材の効果を検証するブログ (grow-child-potential.com)
☆図形と創造力の一歩進んだ学習におすすめ
☆無学年なのでお子様の進捗に合わせた学習
☆8%割引の紹介コードopJTZo1fPgTA


コメント